
*MySQL 버전, 집계 함수(Aggregation) 문제입니다.
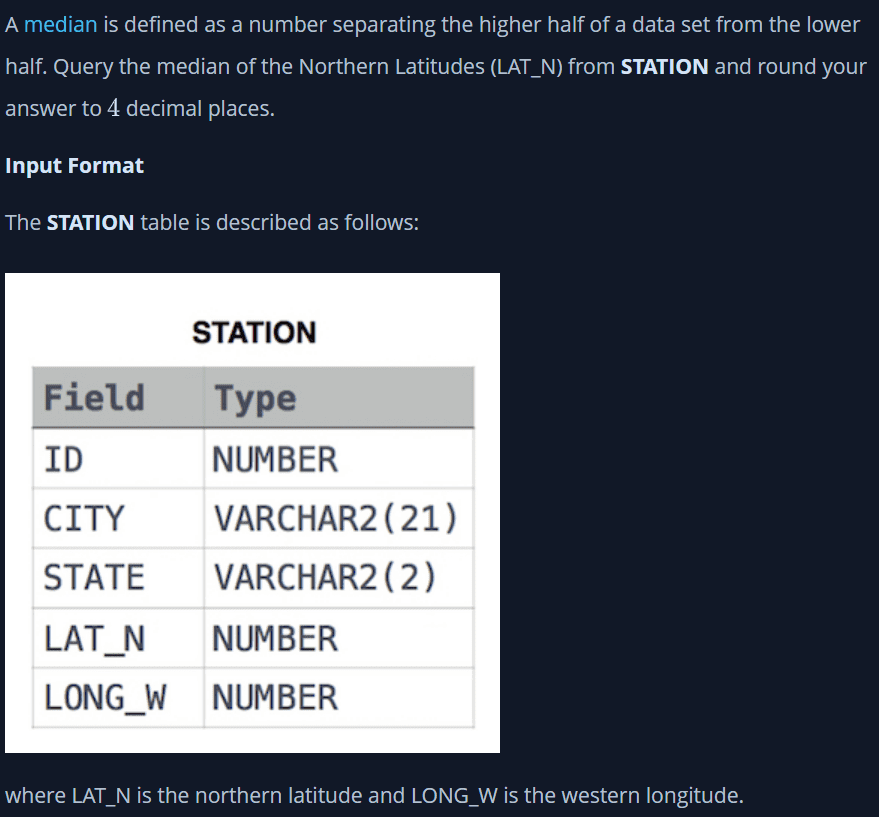
해커랭크 Weather Observation Station 20 문제, 샘플, 설명
- 해당 문제 중앙값(median) 정의: 하위(데이터 셋의 절반)와 상위(데이터 셋의 절반)를 구분하는 정중앙 값
- 소수 4자리까지 반올림 표기
대충 LAT_N의 중앙값을 소수 4자리까지 반올림해서 구하라는 말.
해커랭크 Weather Observation Station 20 답
- PERCENT_RANK() 사용
median은 오름차순 정렬 시 50%인 정중앙 값이다.
그러므로 하위%, 상위%를 구할 수 있는 PERCENT_RANK에서 0.5를 조건으로 걸면 중앙값을 구할 수 있다.
- 인라인 뷰 사용
PECENT_RANK()의 결괏값이 담긴 테이블을 참조.
- ROUND 사용
SELECT ROUND(LAT_N, 4)
FROM (
SELECT *
, PERCENT_RANK() OVER(ORDER BY LAT_N) AS p_r
FROM STATION
) AS aaa
WHERE p_r = 0.5;
추가 정리
- 중앙값Median
값들을 오름차순 정렬 시, 값들이 홀수 개라면 중앙값을 바로 알 수 있다.
=산술평균
반면 값들이 짝수 개라면 중앙의 두 값을 더하고 2로 나눈 것이 중앙값이다.
=산술평균 올림과 내림 값의 평균
*중앙값 reference http://minitistics.tistory.com/3
평균값(Mean), 중앙값(Median), 최빈값(Mode)
'평균'이라는 개념은 우리에게 매우 익숙합니다. 시험점수를 각 과목별로 합한 후, 전체 과목의 수로 나누어 계산한 값, 즉 평균으로 등수가 결정되었죠. 평균값은 이 외에도 대표값으로 사용되
minitistics.tistory.com
row_number() 사용 쿼리
이는 로우마다 매겨진 순번에 해당하는 값의 평균으로 중앙값을 구하는 방법이다.
WITH rn_order AS(
SELECT LAT_N
, ROW_NUMBER() OVER(ODER BY LAT_N) AS r_n
FROM STATION
)
SELECT ROUND(AVG(LAT_N), 4)
FROM rn_order
WHERE r_n = (SELECT FLOOR(AVG(r_n)) FROM rn_order)
OR (SELECT CEIL(AVG(r_n)) FROM rn_order);
이 방법의 관건(?)은 로우가 짝수 개일 경우인데, 쉬운 예를 들면 다음과 같다.
*문제의 실제 데이터 값 아님.
1. WITH는 LAT_N을 기준으로 내림차순 정렬하여, 로우마다 순번을 매긴 테이블(rn_order)이다.
| rn_order | |
| LAT_N | r_n |
| 3 | 1 |
| 6 | 2 |
| 7 | 3 |
| 8 | 4 |
2. 이때 참조할 rn_order의 로우가 짝수 개일 경우를 고려해야 한다.
값이 짝수 개라면 중앙의 두 값을 더하고 2로 나눈 것이 중앙값이다.
=산술평균 올림과 내림 값의 평균
r_n의 산술평균은 2.5이며, 이를 내림하면 2, 올림 하면 3이다.
r_n = 2 혹은 r_n = 3에 해당하는 LAT_N은 6, 7이다.
*이게 서브쿼리 WHERE 조건식에 입력한 rn=FLOOR(~) OR CEIL(~)이다.
- FLOOR(): 정수로 내림
- CEIL(): 정수로 올림
| rn_order | |
| LAT_N | r_n |
| 6 | 2 |
| 7 | 3 |
3. 2에서 필터링된 LAT_N의 값은 6, 7이므로, 두 수의 평균인 중앙값은 6.5이다.
이렇게 로우마다 순번을 매긴 이유는 다음과 같다.
- 위의 쉬운 예시는 데이터가 얼마 되지 않아, 한눈에 LAT_N의 값들이 보이므로 중앙값 계산이 쉽다.
- 하지만 LAT_N 데이터가 굉장히 많다면? 중앙에 어떤 값이 있는지 알기 어렵다.
- 그래서 순번을 매기고 중앙에 있는 두 순번에 해당된 LAT_N 값들을 찾는 것이다.
나로서는 생각할 거리가 많았던 문제였다.
배울 것이 참 많다!
'SQL > HackerRank(해커랭크)' 카테고리의 다른 글
| HackerRank(해커랭크) MySQL The PADS 문제 답 (0) | 2023.10.13 |
|---|---|
| HackerRank(해커랭크) MySQL Type of Triangle 문제 답 (1) | 2023.10.11 |
| HackerRank(해커랭크) MySQL Weather Observation Station 19 문제 답 (2) | 2023.10.06 |
| HackerRank(해커랭크) MySQL Average Population of Each Continent 문제 답 (0) | 2023.10.05 |
| HackerRank(해커랭크) MySQL Top Earners 문제 답 (0) | 2023.10.04 |
